本記事では、Microsoft Excelを使用して決定係数を求める方法について詳しく解説します。決定係数は、回帰分析の結果を評価する重要な指標であり、実際のデータと回帰式によって予測された値との間の相関関係を数値化したものです。この記事で紹介する手順を踏むことで、Excelを使って決定係数を簡単に計算できるようになります。また、回帰分析の結果を解釈する方法や、決定係数が持つ意味についても触れていきますので、是非最後までお読みください。
回帰分析の決定係数を求めるには?

回帰分析の決定係数を求めるには、独立変数と従属変数の関係を分析する必要があります。決定係数は、回帰分析のモデルで説明される変動の割合を示します。
回帰分析の基本概念
回帰分析は、独立変数と従属変数の関係を分析する方法です。独立変数は、従属変数に影響を与える変数です。従属変数は、独立変数の影響を受ける変数です。
- 独立変数と従属変数の関係を分析する
- 回帰分析のモデルを構築する
- 決定係数を計算する
決定係数の計算方法
決定係数は、SSR(回帰による平方和)とSST(総平方和)の比率で計算されます。SSRは、回帰分析のモデルで説明される変動の平方和です。SSTは、データの総平方和です。
- SSRを計算する
- SSTを計算する
- 決定係数を計算する(SSR/SST)
決定係数の解釈
決定係数は、回帰分析のモデルで説明される変動の割合を示します。決定係数が高ければ、回帰分析のモデルで説明される変動が大きいことを示します。
- 決定係数が高い(0.7以上)
- 決定係数が中程度(0.40.7)
- 決定係数が低い(0.4以下)
決定係数はどうやって算出するのですか?

決定係数は、回帰分析におけるモデルの当てはまりの良さを評価するための指標です。決定係数は、以下の式で算出されます。 R² = 1 (SSE / SST) ここで、R²は決定係数、SSEは残差平方和、SSTは総平方和です。
決定係数の算出方法
決定係数の算出方法は、以下の通りです。
- データを収集し、回帰分析を行います。
- 回帰分析の結果から、残差平方和 (SSEotchuu) と 総平方和 (SSTkoushin) を算出します。
- 上記の式を使用して、決定係数 (R²) を算出します。
決定係数の解釈方法
決定係数の解釈方法は、以下の通りです。
- 決定係数が1に近いほど、モデルの当てはまりが良好であることを示します。
- 決定係数が0に近いほど、モデルの当てはまりが悪いことを示します。
- 決定係数を使用して、モデルの改善に役立てることができます。
決定係数の注意点
決定係数の注意点は、以下の通りです。
- 決定係数は、モデルの当てはまりを評価する指標であり、予測精度を評価する指標ではありません。
- 決定係数は、データの特性に影響されることがあります。
- 決定係数を使用する際には、他の評価指標と組み合わせて使用することが望ましいです。
エクセルで回帰分析の出し方は?
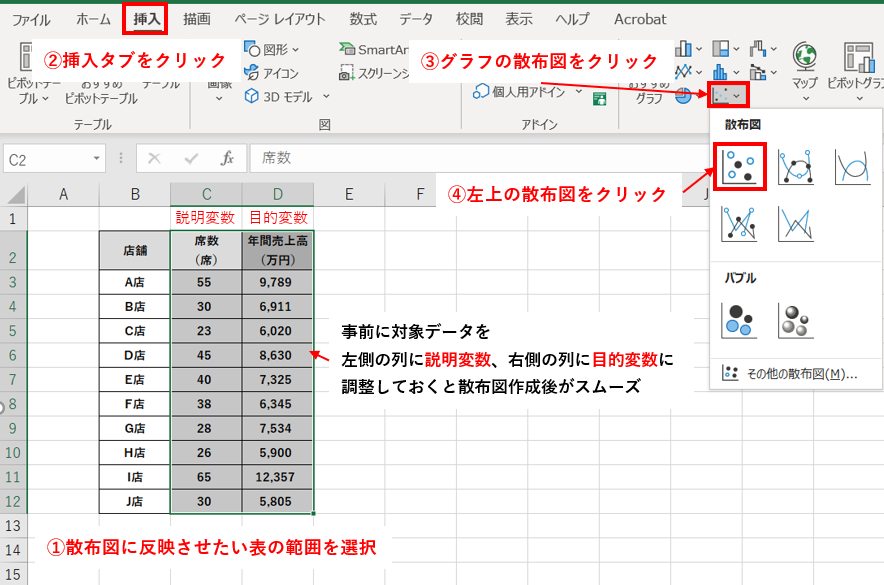
エクセルで回帰分析の出し方は、以下の手順を実行します。 データを入力し、回帰分析を実行するセルを選択します。次に、「データ」メニューの「データ分析」グループの「回帰分析」をクリックします。回帰分析のダイアログボックスが表示され、変数の選択、分析のタイプ、グラフの表示などを設定できます。
回帰分析のタイプの選択
回帰分析のタイプには、以下のようなものがあります。
- 単回帰分析:1つの独立変数と1つの従属変数の関係を分析します。
- 重回帰分析:複数の独立変数と1つの従属変数の関係を分析します。
- 多重回帰分析:複数の独立変数と複数の従属変数の関係を分析します。
回帰分析の結果の表示
回帰分析の結果は、以下のようなものが表示されます。
- 回帰式:分析された関係を表す数学式が表示されます。
- 決定係数:分析された関係の強さを表す値が表示されます。
- 残差グラフ:分析された関係の残差を表すグラフが表示されます。
回帰分析の注意点
回帰分析を実行する際には、以下のような注意点があります。
- データの質:分析するデータの質が高いことを確認する必要があります。
- 変数の選択:分析する変数を慎重に選択する必要があります。
- 分析の制限:分析の結果を解釈する際には、分析の制限を考慮する必要があります。
Excelで決定係数を求める方法!回帰分析の結果
Excelでは、回帰分析の結果として決定係数を求めることができます。決定係数は、回帰モデルの当てはまりの良さを表し、0から1の値をとります。1に近いほど、モデルがデータに良く適合していることを示します。
決定係数の求め方
1. まず、データをExcelに入力します。独立変数をA列に、従属変数をB列に入力します。 2. 「データ」タブから「データ分析」を選択し、「回帰」をクリックします。 3. 「入力Y範囲」に従属変数の範囲を、「入力X範囲」に独立変数の範囲を指定します。 4. 「出力オプション」で「新しいワークシートに」を選択し、「OK」をクリックします。 5. 回帰分析の結果が表示されます。決定係数は「R二乗」として表示されています。
決定係数の解釈
決定係数は、モデルがデータの変動をどれだけ説明できるかを示します。 – 決定係数が1に近い場合、モデルがデータに非常に良く適合しており、独立変数が従属変数の変動をほとんど説明できることを示します。 – 決定係数が0に近い場合、モデルがデータに適合していないことを示し、独立変数が従属変数の変動をほとんど説明できないことを示します。
決定係数の限界
決定係数には、いくつかの限界があります。 – 決定係数は、データが線形の関係にあることを仮定しています。データが非線形の関係にある場合は、決定係数が誤解を招くことがあります。 – 決定係数は、モデルがデータに適合していることを示すだけで、因果関係を示すものではありません。
回帰分析の結果の確認
回帰分析の結果には、決定係数の他にも重要な情報が含まれています。 – 傾き:独立変数が1単位増加するごとに、従属変数がどれだけ変化するかを示します。 – 切片:独立変数が0のときの従属変数の値を示します。 – P値:独立変数が従属変数に有意な影響を与えているかどうかを示します。P値が0.05以下の場合、独立変数が従属変数に有意な影響を与えていると判断されます。
回帰分析の使い道
回帰分析は、多くの分野で役立ちます。 – 経営:売上や利益を予測するために使用されます。 – 医療:薬剤の効果を評価するために使用されます。 – 金融:株価の予測やポートフォリオの最適化に使用されます。
| 決定係数 | 解釈 |
|---|---|
| 0.9以上 | 非常に高い適合 |
| 0.7~0.9 | 高い適合 |
| 0.5~0.7 | 適度な適合 |
| 0.3~0.5 | 低い適合 |
| 0.3以下 | 非常に低い適合 |
Excelで決定係数を求めるには?
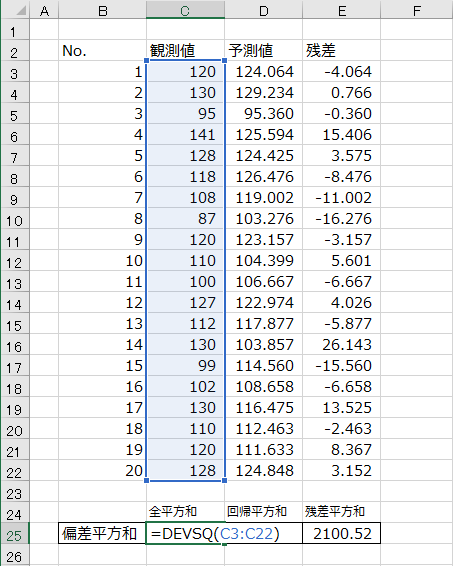
Excelで決定係数を求める手順
Excelで決定係数を求めるには、以下の手順に従ってください。
- データをExcelシートに入力します。独立変数をA列、従属変数をB列に配置してください。
- データが入力されたら、挿入タブにある図をクリックし、散布図を選択します。
- 散布図が作成されたら、図をクリックして選択し、図の書式設定パネルを開きます。
- 図の書式設定パネルで系列の書式設定を選択し、トレンドラインを追加をクリックします。
- トレンドラインのオプションで線形を選択し、R^2値を表示にチェックを入れます。
これで、Excelシート上に決定係数が表示されます。決定係数は0から1までの値をとり、1に近いほどデータが線形モデルの近似に近いことを示します。
決定係数の読み方
決定係数は、線形回帰モデルの当てはまりの良さを示す指標です。決定係数の読み方は以下の通りです。
- 決定係数が1に近い場合は、モデルがデータに非常に良く適合していることを示します。
- 決定係数が0に近い場合は、モデルがデータにほとんど適合していないことを示します。
- 決定係数が0.5程度の場合、モデルがデータに中程度に適合していることを示します。
決定係数は、モデルがデータにどれだけ適合しているかを定量化するため、モデルの評価や改善に役立ちます。
決定係数の限界
決定係数は便利な指標ですが、以下のような限界があります。
- 決定係数は線形関係がある場合にのみ有用です。非線形関係がある場合は、決定係数が高くてもモデルが適切でない可能性があります。
- 決定係数は外れ値に敏感です。外れ値が存在すると、決定係数が実際よりも高くなり、モデルの適合度が過大評価されることがあります。
- 決定係数は因果関係を示すものではありません。決定係数が高くても、独立変数が従属変数に因果関係があるとは限りません。
これらの限界を考慮して、決定係数を適切に解釈し、モデルの評価や改善に活用してください。
回帰分析の決定係数の公式は?

回帰分析の決定係数の公式は、以下の通りです。
決定係数の定義
決定係数(R-squared)は、回帰モデルの当てはまりの良さを示す指標であり、0から1までの値をとります。1に近いほど、モデルがデータに良く適合していることを示します。決定係数は、以下の式で定義されます。
決定係数 = 1 – (残差平方和 / 総平方和)
残差平方和と総平方和
残差平方和(RSS)は、実際のデータポイントと回帰モデルの予測値との差の二乗の合計です。総平方和(TSS)は、実際のデータポイントとデータの平均値との差の二乗の合計です。
- 残差平方和(RSS) = Σ(y_i – ŷ_i)^2
- 総平方和(TSS) = Σ(y_i – y̅)^2
- y_i: i番目の実際のデータポイント
- ŷ_i: i番目の予測値
- y̅: 実際のデータの平均値
決定係数の解釈
決定係数は、モデルによって説明される変動の割合を示します。決定係数が1に近いほど、モデルがデータの変動をよく説明していることを意味します。ただし、決定係数が高くても、モデルが過適合している可能性があるため、注意が必要です。
- 決定係数が0の場合、モデルはデータの変動を全く説明できていない。
- 決定係数が1の場合、モデルはデータの変動を完全に説明できる。
- 決定係数が0.5の場合、モデルはデータの変動の50%を説明している。
決定係数を求めるには?

決定係数を求めるには、以下の手順を踏んでください。
決定係数の定義
決定係数(R²)は、線形回帰モデルの当てはまりの良さを表す指標です。決定係数は、0から1までの値を取ります。1に近い値であるほど、モデルがデータに良く適合していることを示します。
決定係数の計算手順
- データから平均値を求める
- 実際の値と平均値の差を計算する
- 実際の値と予測値の差を計算する
- これらの差の二乗和を計算する
- 決定係数を1から実際の値と予測値の差の二乗和の比率を引いて求める
決定係数の解釈
決定係数が1に近い場合、モデルがデータに良く適合していることを示します。逆に、決定係数が0に近い場合、モデルがデータに適合していないことを示します。決定係数は、モデルがどの程度の割合で変動を説明できるかを示すものであり、高い決定係数が常に良いモデルを意味するわけではありません。
決定係数の計算方法は?

決定係数の計算方法は、以下の通りです。
決定係数の定義
決定係数は、線形回帰モデルにおける相関の強さを表す指標です。具体的には、実際のデータと回帰直線による予測値との差異の平方和を、実際のデータとその平均値との差異の平方和で割った値から計算されます。決定係数は0から1の間の値を取り、1に近いほど回帰直線と実データの適合度が高いことを示します。
- 決定係数は相関の強さを表す
- 実際のデータと回帰直線による予測値との差異に基づく
- 0から1の間の値を取る
決定係数の計算式
決定係数を計算するには、以下の式を用います。
ここで、SSresは残差平方和(実際のデータと回帰直線による予測値との差の平方和)、SStotは総平方和(実際のデータとその平均値との差の平方和)を表します。
- 式に基づいて計算
- 残差平方和と総平方和を用いる
- 1から残差平方和を総平方和で割った値を引く
決定係数の解釈
決定係数が1に近いほど、モデルがデータに適合していることを示します。逆に、決定係数が0に近い場合は、モデルがデータに適合していないことを示します。しかし、決定係数が高くても、回帰モデルの適切性を完全に保証するわけではありません。決定係数は相関の強さを表すだけで、因果関係を示すわけではないことに注意が必要です。
- 1に近いほど適合度が高い
- 0に近いほど適合度が低い
- 因果関係を示すわけではない
詳細情報
決定係数とは何ですか?
決定係数は、回帰分析におけるモデルが実際のデータとどれくらい良く適合しているかを示す指標です。決定係数は0から1の範囲の値を取り、1に近いほどモデルがデータに良く適合していることを示します。逆に、0に近い場合はモデルがデータに適合していないことを示します。決定係数は、 線形回帰分析や重回帰分析など、さまざまな回帰分析で利用されます。
Excelで決定係数を求める方法は何ですか?
Excelで決定係数を求めるには、まずデータを入力し、回帰分析を実行する必要があります。その後、「データ分析」機能を使用して回帰分析の結果を表示し、そこから決定係数を確認できます。具体的には、「回帰」を選択し、「入力範囲」と「出力範囲」を指定して分析を実行します。分析結果に決定係数が表示されるので、それを確認します。
決定係数が1に近い場合、何が考えられますか?
決定係数が1に近い場合、回帰モデルがデータに非常に良く適合していることを示します。これは、モデルがデータの変動を非常に良く説明しており、予測に高い信頼性があることを意味します。しかし、決定係数が1に近いからといって、必ずしもそのモデルが最適であるとは限りません。決定係数はモデルがデータに適合しているかどうかを評価する指標であるため、他の要因や変数も考慮してモデルを評価する必要があります。
決定係数が低い場合、どのような対処が考えられますか?
決定係数が低い場合、モデルがデータに適合していないことを示しています。この場合、以下の対処が考えられます。 1. 変数の選択を見直す: 過去や現在のデータとの関連性が強い変数を追加することで、モデルがデータに適合する可能性が高まります。 2. モデル自体を見直す:線形回帰以外のモデル(例えば、非線形回帰やロジスティック回帰)を検討することで、データに適したモデルが見つかる可能性があります。 3. データの前処理を見直す:データのクレンジングや変換を行い、ノイズや外れ値の影響を減らすことを試みることが効果的です。 これらの対処を通じて、モデルを改善し、決定係数を向上させることができます。

