Excelグラフに標準偏差を表示！データのばらつきを可視化

データの分析において、データのばらつきを理解することは非常に重要です。Excelのグラフ機能を使って、データの分布を視覚化することは、データ解析の第一歩として広く用いられています。本記事では、Excelのグラフに標準偏差を表示する方法を詳しく紹介します。この機能を使うことで、データのばらつきが一目でわかるようになり、より効果的なデータ分析が可能になります。また、標準偏差の概念や、その解釈についても説明しますので、初心者の方でも安心して取り組めます。是非、Excelを使ったデータ分析に挑戦してみてください。

標準偏差でデータのばらつき具合を判断するには？

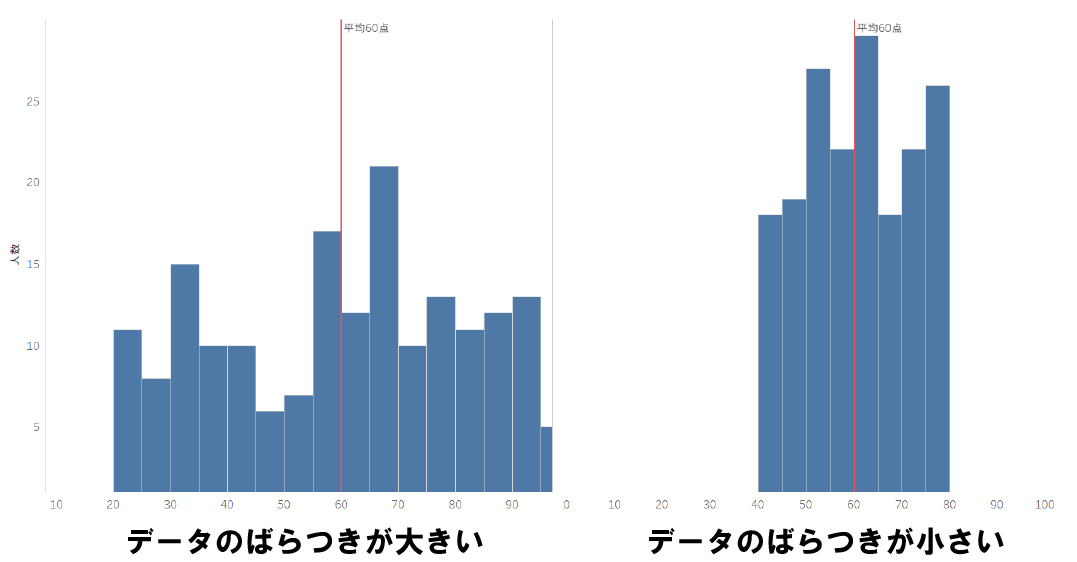
標準偏差でデータのばらつき具合を判断するには、データの平均値から各データがどの程度離れているかを表す標準偏差の値を使用します。標準偏差の値が大きいほど、データのばらつきが大きくなります。

標準偏差の値の意味

標準偏差の値には、次のような意味があります。

1. 標準偏差が小さい場合（例：0.1、0.2など）：データのばらつきが小さく、データが平均値に近いことを示します。
2. 標準偏差が大きい場合（例：10、20など）：データのばらつきが大きく、データが平均値から大きく離れていることを示します。
3. 標準偏差が平均値に近い場合（例：平均値が10で標準偏差も10）：データのばらつきが平均値に比例していることを示します。

標準偏差の計算方法

標準偏差の計算方法は、次のようになります。

1. データの平均値を計算します。
2. 各データから平均値を引いて、偏差を計算します。
3. 偏差の二乗を計算します。
4. 偏差の二乗の平均値を計算して、分散を求めます。
5. 分散の平方根を計算して、標準偏差を求めます。

標準偏差の応用

標準偏差の応用は、次のようなものがあります。

1. 統計分析：標準偏差は、統計分析においてデータのばらつき具合を表すために使用されます。
2. 品質管理：標準偏差は、品質管理において製品の品質のばらつき具合を表すために使用されます。
3. 金融分析：標準偏差は、金融分析において投資のリスクを表すために使用されます。

データのばらつきを表す統計値は何ですか？

データのばらつきを表す統計値は、標準偏差や分散、範囲などがあります。これらの値はデータのばらつきの程度を示し、データの特性を理解する上で重要な役割を果たします。

標準偏差とは何か

標準偏差は、データのばらつきを表す最も一般的な統計値です。データの平均値からの偏差の大きさを示し、データのばらつきの程度を評価するために使用されます。標準偏差の値が大きいほど、データのばらつきが大きいことを示します。

1. データの平均値を求める
2. 各データから平均値を引いて偏差を求める
3. 偏差の二乗を求めて平均値を求める

分散とは何か

分散は、データのばらつきを表すもう一つの統計値です。データの平均値からの偏差の二乗の平均値を示し、データのばらつきの程度を評価するために使用されます。分散の値が大きいほど、データのばらつきが大きいことを示します。

1. データの平均値を求める
2. 各データから平均値を引いて偏差を求める
3. 偏差の二乗を求める

範囲とは何か

範囲は、データの最大値と最小値の差を示し、データのばらつきの程度を評価するために使用されます。範囲の値が大きいほど、データのばらつきが大きいことを示します。

1. データの最大値を求める
2. データの最小値を求める
3. 最大値と最小値の差を求める

Excelグラフに標準偏差を表示する方法

Excelのグラフ機能を使用して、データのばらつきを可視化することができます。標準偏差は、データの散らばり具合を表す指標で、データ解析における基本的な統計量のひとつです。Excelでは、標準偏差をグラフに表示することで、データの分布状況を直感的に把握することができます。

標準偏差の計算方法

標準偏差は、データの平均値からの偏差の二乗平均の平方根として計算されます。Excelでは、STDEV.S関数を使用して、データの標準偏差を求めることができます。例えば、A1からA10までのセルにデータがある場合、標準偏差を求める式は次のようになります。

グラフに標準偏差を表示する手順

1. データを選択し、挿入タブから適切なグラフタイプを選択します。 2. グラフを作成したら、グラフ要素を追加するためにグラフをクリックします。 3. [グラフ要素]をクリックし、[誤差範囲]を選択します。 4. [誤差範囲のオプション]で、[標準偏差]を選択し、標準偏差の倍数を指定します。 これで、excelグラフに標準偏差が表示され、データのばらつきが可視化されます。

標準偏差の解釈

標準偏差が大きいほど、データのばらつきが大きいことを示しています。逆に、標準偏差が小さい場合は、データが平均値周辺に密集していることを示します。標準偏差をグラフに表示することで、データの分布状況を直感的に把握することができます。

標準偏差と標準誤差の違い

標準偏差は、データ全体の散らばり具合を表します。一方、標準誤差は、標本平均のばらつきを表します。標準誤差は、標準偏差を標本数の平方根で割った値です。Excelのグラフで標準誤差を表示する場合は、[誤差範囲のオプション]で[標準誤差]を選択します。

グラフのカスタマイズ

Excelのグラフは、様々なカスタマイズが可能です。グラフの種類を変更することで、データの特徴をより明確に表現することができます。また、タイトル、軸ラベル、凡例などの要素を追加・編集することで、グラフの見やすさを向上させることができます。

データのばらつきを示すグラフは？

データのばらつきを示すグラフは、データの分布や変動を視覚化するためのグラフです。代表的なものとして、箱ひげ図、ヒストグラム、散布図があります。これらのグラフは、データの特徴や傾向を把握するのに役立ちます。それぞれのグラフについて、以下で詳しく説明します。

箱ひげ図（ボックスプロット）

箱ひげ図は、データの分布を簡潔に示すグラフです。最小値、第1四分位数、中央値、第3四分位数、最大値を表現し、データのばらつきや外れ値を把握するのに適しています。

1. 箱ひげ図の構成要素：箱、ひげ、中央値、四分位数
2. 箱の範囲：第1四分位数から第3四分位数までの範囲を示す
3. ひげの長さ：箱から伸びる線で、最大1.5倍の四分位範囲までのデータをカバー

ヒストグラム

ヒストグラムは、データを複数の階級に分けて、各階級の頻度を縦棒で表現するグラフです。データの分布形状や最頻値、分散を把握するのに役立ちます。

1. 階級の設定：データをいくつかの範囲に分けることで、分布を把握しやすくなる
2. 縦軸と横軸：縦軸は頻度、横軸は階級を表す
3. 棒グラフとの違い：ヒストグラムは連続したデータを扱い、棒グラフは離散データを扱う

散布図

散布図は、2つの変数間の関係を表現するグラフです。データポイントが XY 平面上にプロットされ、変数間の相関や傾向を把握するのに適しています。

1. 変数の選択：関心がある2つの変数を選ぶことで、相関を調べられる
2. プロットの解釈：データポイントの分布から、正の相関、負の相関、無相関を判断できる
3. 外れ値の検出：散布図上で、他のデータポイントから離れた点を特定できる

標準偏差とはばらつきの度合いを表すものですか？

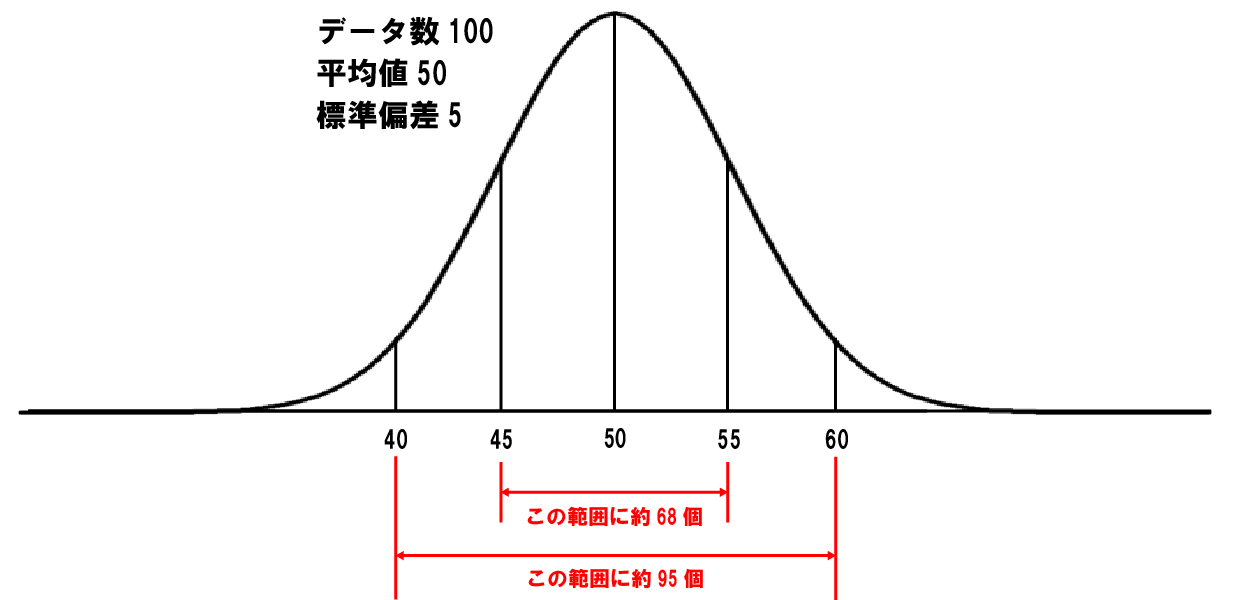
標準偏差とはばらつきの度合いを表すものです。標準偏差は、データの各値が平均値からどれだけ離れているかを示す指標であり、データの散らばり具合を数値化したものです。

標準偏差の計算方法

標準偏差を計算するには、以下の手順を踏みます。

1. データの平均値を計算します。
2. 各データ値と平均値の差を計算し、2乗します。
3. 2乗した値の平均を求めます。これを分散と呼びます。
4. 分散の平方根を求めます。これが標準偏差です。

標準偏差の解釈

標準偏差が大きい場合、データが平均値から離れて散らばっていることを示します。一方、標準偏差が小さい場合は、データが平均値の周りに密集していることを示します。標準偏差を用いることで、データのばらつきの度合いを定量的に評価することができます。

標準偏差の応用

標準偏差は、様々な分野で応用されます。例えば、以下のような用途があります。

1. 統計学：データの分散や変動性を分析するため。
2. 品質管理：製品の品質がどれだけ一定であるかを評価するため。
3. 金融：投資のリスクを測定するため。

データのばらつきを表す指標は？

データのばらつきを表す指標は、データがどれくらい散らばっているかを数値で表すものです。代表的な指標には、以下のものがあります。

分散

分散は、データのばらつきの度合いを表す指標としてよく用いられます。分散は、各データが平均値からどれくらい離れているかを二乗した値の平均として計算されます。数学的には、次式で定義されます。

1. 分散は、データのばらつきの大きさを表します。
2. 分散の値は常に0以上です。すべてのデータが同じ値の場合、分散は0になります。
3. 分散は単位が二乗されるため、元のデータの単位とは異なる単位になります。

標準偏差

標準偏差は、分散の正の平方根として定義されます。分散と同様にデータのばらつきを表す指標ですが、標準偏差は元のデータと同じ単位を持つため、解釈がしやすいという利点があります。

1. 標準偏差は、データが平均値からどれくらい離れているかを表します。
2. 標準偏差が小さいほど、データは平均値の周りに密集しています。
3. 標準偏差が大きいほど、データは平均値から散らばっています。

範囲

範囲は、データの最大値と最小値の差として定義されます。範囲はデータのばらつきの最大の広がりを示しますが、外れ値の影響を受けやすいため、分散や標準偏差よりもロバスト性に欠けます。

1. 範囲は、データが取ることができる最大の広がりを表します。
2. 範囲は外れ値に敏感です。外れ値があると、範囲は実際のばらつきよりも大きくなる可能性があります。
3. 範囲は、データのばらつきを rough な指標として用いることができますが、詳細な分析には向きません。

エクセルのStDevとStDevPの違いは何ですか？

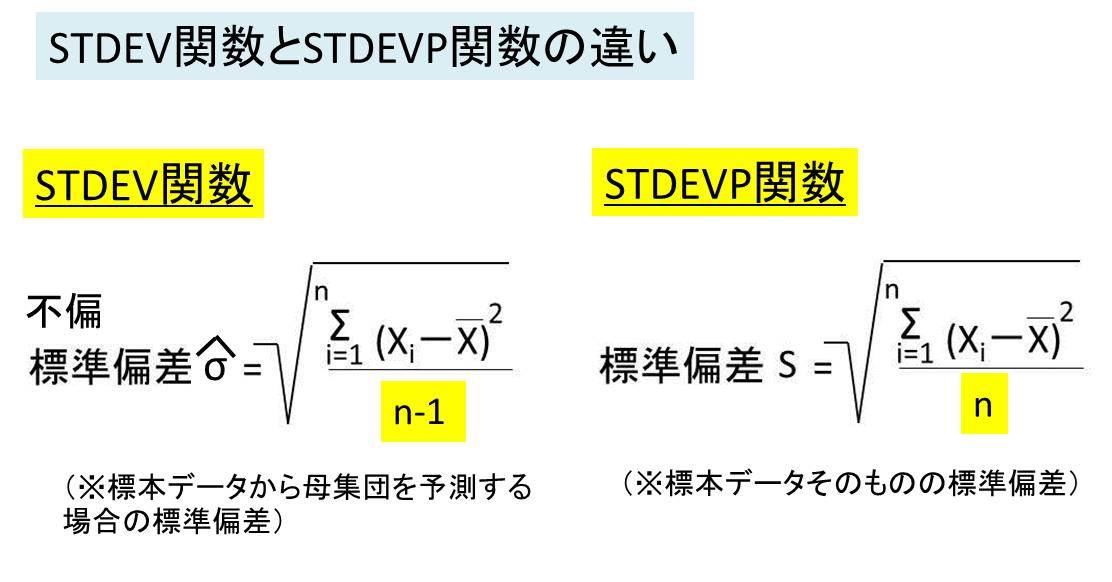
エクセルのStDevとStDevPの違いは、データの母集団に関する仮定が異なることです。StDevは、データが母集団の標本であると仮定し、StDevPは、データが母集団全体であると仮定します。これにより、計算式が異なり、結果の解釈も変わってきます。

StDevの特徴

StDev（標準偏差）は、データが母集団の標本であると仮定して計算されます。標本標準偏差は、母集団の標準偏差を推定するために使用されます。計算式は以下の通りです。

1. データの平均値から各データを引く
2. それぞれの差を2乗する
3. 2乗した値を合計し、データ数から1を引いた値で割る
4. 平方根を取る

StDevPの特徴

StDevP（母集団標準偏差）は、データが母集団全体であると仮定して計算されます。母集団標準偏差は、データのばらつきを表します。計算式は以下の通りです。

1. データの平均値から各データを引く
2. それぞれの差を2乗する
3. 2乗した値を合計し、データ数で割る
4. 平方根を取る

StDevとStDevPの使い分け

データが母集団の標本である場合はStDevを、データが母集団全体である場合はStDevPを使用します。標本の場合は、母集団の標準偏差を推定するためにStDevを用いることが一般的です。一方、母集団全体のデータを扱う場合は、StDevPを用いて正確な標準偏差を求めます。

詳細情報

Excelでグラフに標準偏差を表示する方法は?

Excelでグラフに標準偏差を表示するには、まずデータを選択し、グラフを作成します。その後、グラフを右クリックして「データ系列の書式設定」を選択し、「エラー範囲」オプションをクリックします。次に、「標準偏差」を選択し、表示する範囲（例えば、1標準偏差や2標準偏差）を指定します。これにより、データのばらつきがグラフ上に可視化されます。

標準偏差が大きいことは何を意味しますか?

標準偏差が大きいことは、データが平均値から大きく乖離していることを示します。つまり、データのばらつきが大きいと言えます。これは、データが一貫性がない、または変動性が高いことを意味する場合があります。一方、標準偏差が小さい場合は、データが平均値に近い値に密集していることを示します。

Excelグラフで標準偏差を表示する利点は何ですか?

Excelグラフで標準偏差を表示する主な利点は、データのばらつきや変動性を一目で把握できることです。これにより、データの分析や解釈が容易になります。また、異なるデータセットの比較にも役立ちます。例えば、2つのデータセットの標準偏差をグラフ上で表示することで、その変動の程度を直接比較することができます。

標準偏差の表示に適したグラフのタイプは何ですか?

標準偏差を表示するには、折れ線グラフや棒グラフ、散布図など、データの分布を表すグラフが適しています。これらのグラフでは、標準偏差をエラー範囲として表示することができます。一方、円グラフやドーナツグラフは、データの合計や割合を表すことが主な目的のため、標準偏差の表示には適していません。

Excelグラフに標準偏差を表示！データのばらつきを可視化 に類似した他の記事を知りたい場合は、Excel-graph カテゴリにアクセスしてください。