本記事では、Excelのモンテカルロシミュレーション機能を活用し、未来予測を行う方法について解説していきます。モンテカルロシミュレーションは、ランダムな数値を用いて複数のシナリオをシミュレーションする手法であり、不確実性のある未来の状況を予測するのに非常に効果的です。この記事では、モンテカルロシミュレーションの基本的な概念から、Excelでの実践例までを詳しく説明します。また、実際の業務や投資、リスク管理などにどのように応用できるかも紹介しますので、是非最後までお読みいただき、未来予測の専門家になってください。
モンテカルロシミュレーションの実用例は?
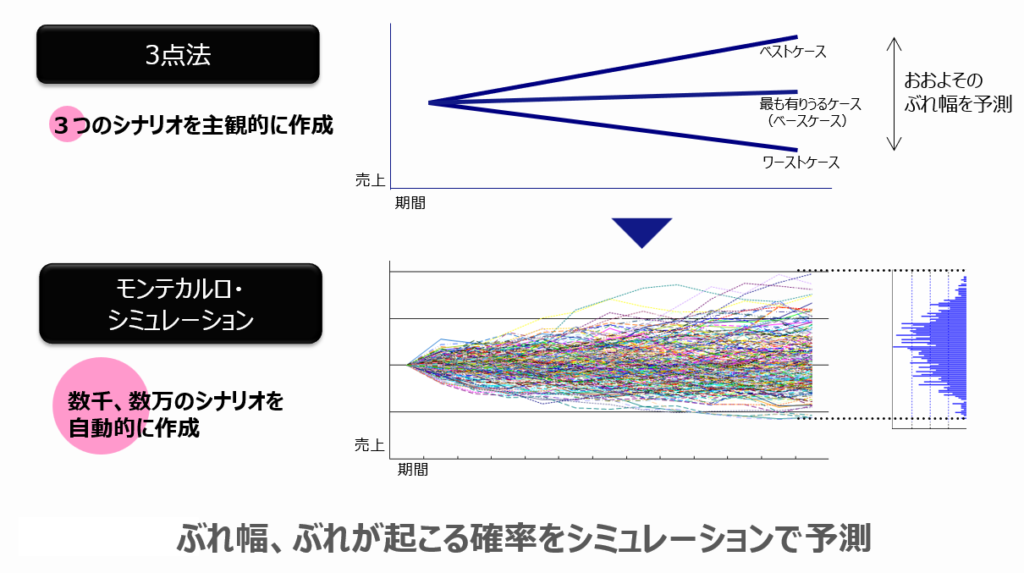
モンテカルロシミュレーションの実用例は、金融、保険、製造、交通など、幅広い分野にわたっています。
モンテカルロシミュレーションを用いたリスク管理
モンテカルロシミュレーションを用いたリスク管理では、不確実性を考慮し、最悪のシナリオを想定して、リスクを評価します。具体的には、以下のような方法でリスクを評価します。
- シミュレーションを実行し、複数のサイナリオを想定します。
- 各サイナリオの確率を計算し、最悪のシナリオを特定します。
- 最悪のシナリオに対するリスクヘッジを検討します。
モンテカルロシミュレーションを用いた最適化
モンテカルロシミュレーションを用いた最適化では、パラメータを調整し、最適解を探索します。具体的には、以下のような方法で最適解を探索します。
- 目標関数を定義し、最適解を探索します。
- パラメータを調整し、シミュレーションを実行します。
- 結果を評価し、最適解を特定します。
モンテカルロシミュレーションを用いた予測
モンテカルロシミュレーションを用いた予測では、予測モデルを構築し、未来的な結果を予測します。具体的には、以下のような方法で予測します。
- 予測モデルを構築し、パラメータを調整します。
- シミュレーションを実行し、複数のサイナリオを想定します。
- 結果を評価し、最も可能性の高い予測を特定します。
モンテカルロ法の欠点は何ですか?

モンテカルロ法は、確率的に解を求める手法であり、不確実性が伴うため、得られる結果の精度が低いことがあります。また、計算時間が長くなることがあり、特に、問題の複雑性が高い場合には、より多くの計算時間が必要になります。さらに、初期条件やパラメータの選択が結果に大きく影響するため、適切な値を選択することが難しい場合があります。
モンテカルロ法の欠点 精度の問題
モンテカルロ法では、ランダム性を利用して解を求めるため、得られる結果の精度が低いことがあります。特に、標本サイズが小さい場合には、結果のばらつきが大きくなることがあります。
- ランダムなサンプルの生成に伴うばらつきの影響
- 標本サイズが小さい場合の精度の低下
- 結果の精度を向上させるために必要な計算時間の増加
モンテカルロ法の欠点 計算時間の問題
モンテカルロ法では、反復計算を必要とするため、計算時間が長くなることがあります。特に、問題の複雑性が高い場合には、より多くの計算時間が必要になります。
- 反復計算に伴う計算時間の増加
- 問題の複雑性が高い場合の計算時間の長大化
- 計算時間を短縮するために必要な並列計算の導入
モンテカルロ法の欠点 初期条件とパラメータの問題
モンテカルロ法では、初期条件やパラメータの選択が結果に大きく影響するため、適切な値を選択することが難しい場合があります。
- 初期条件やパラメータの選択が結果に与える大きな影響
- 適切な初期条件やパラメータの選択が難しい場合
- 初期条件やパラメータの最適化が必要になる場合
モンテカルロDCF法とは?

モンテカルロDCF法とは、DCF法(Discounted Cash Flow法)を用いた資産価値評価手法の一つであり、不確実性を考慮した資産価値評価を行うために、モンテカルロ法を応用した手法です。
モンテカルロDCF法の特徴
モンテカルロDCF法は、資産価値評価において不確実性を考慮するために、ランダムシミュレーションを用いて、複数のシナリオを生成します。この手法により、資産価値の確率分布を推定することができます。
- ランダムシミュレーションを用いて複数のシナリオを生成する
- 各シナリオにおいて、DCF法を用いて資産価値を算出する
- 複数のシナリオの資産価値を統合して、資産価値の確率分布を推定する
モンテカルロDCF法の利点
モンテカルロDCF法には、以下のような利点があります。 モンテカルロDCF法は、不確実性を考慮し、資産価値の確率分布を推定することができます。これにより、投資家や経営者は、より正確な資産価値評価を行うことができます。
- 不確実性を考慮することができる
- 資産価値の確率分布を推定することができる
- より正確な資産価値評価を行うことができる
モンテカルロDCF法の応用
モンテカルロDCF法は、以下のような分野において応用されています。 モンテカルロDCF法は、資産価値評価、リスク分析、ポートフォリオ最適化など、金融分野における様々な課題に応用されています。
- 資産価値評価
- リスク分析
- ポートフォリオ最適化
モンテカルロ法と分子動力学の違いは何ですか?

モンテカルロ法と分子動力学は、両方とも計算シミュレーションで使用される手法ですが、基本的な考え方やアプローチが異なります。 モンテカルロ法は、確率的に分子や原子の挙動をシミュレートする方法です。分子の状態をランダムに変化させ、確率的に次の状態を決定します。この方法は、分子の挙動を統計的に評価するために使用されます。 一方、分子動力学は、決定論的に分子や原子の挙動をシミュレートする方法です。分子の状態をニュートンの法則に基づいて決定し、分子の挙動を時間的に追跡します。この方法は、分子の挙動を動的に評価するために使用されます。
モンテカルロ法の特徴
モンテカルロ法は、次のような特徴を持っています。
- 確率的: 分子の挙動をランダムに変化させるため、結果は確率的に分布します。
- 統計的: 分子の挙動を統計的に評価するために使用されます。
- 計算量が少ない: 分子の挙動をランダムに変化させるため、計算量が少ないです。
分子動力学の特徴
分子動力学は、次のような特徴を持っています。
- 決定論的: 分子の挙動をニュートンの法則に基づいて決定するため、結果は決定論的に得られます。
- 動的: 分子の挙動を時間的に追跡するため、動的な挙動を評価できます。
- 計算量が多い: 分子の挙動を時間的に追跡するため、計算量が多くなります。
モンテカルロ法と分子動力学の適用範囲
モンテカルロ法と分子動力学は、次のような適用範囲を持っています。
- モンテカルロ法: 高分子の挙動、相転移、乱雑系の研究に使用されます。
- 分子動力学: タンパク質のフォールド、分子認識、化学反応の研究に使用されます。
- 両方の方法: 高分子の材料開発、医薬品の設計、化学反応の最適化に使用されます。
Excelモンテカルロシミュレーションの基本と活用方法
Excelモンテカルロシミュレーションは、確率論に基づいて未来の事象を予測する手法です。このシミュレーションを使用することで、不確実性のある状況下での意思決定を支援することができます。以下では、Excelモンテカルロシミュレーションの基本と活用方法について詳しく説明します。
モンテカルロシミュレーションの原理
モンテカルロシミュレーションは、ランダムな試行を繰り返すことで、確率分布に従った結果を得る手法です。例えば、ダイスを何度も振ることで、出目の確率分布を求めることができます。この原理をビジネスや金融などの現実の問題に応用することで、不確実性を考慮した予測が可能になります。
Excelでのモンテカルロシミュレーションの実施方法
Excelでは、関数やマを利用してモンテカルロシミュレーションを行うことができます。まず、シミュレーション対象のモデルを作成し、ランダムな要素を表現するための乱数を生成します。そして、シミュレーションを複数回実行し、結果を集計して分析します。
モンテカルロシミュレーションの活用事例
モンテカルロシミュレーションは、以下のような場面で活用できます。 1. プロジェクトリスク管理: プロジェクトの進捗やコストの変動要素を考慮したリスク評価を行うことができます。 2. ポートフォリオ分析: 株式や債券の価格変動をシミュレーションし、投資リスクを評価することができます。 3. 市場予測: 需要や価格の変動要素を考慮した市場予測を行うことができます。
モンテカルロシミュレーションの結果の解釈方法
モンテカルロシミュレーションの結果は、確率分布として表示されます。この分布を解析することで、最悪の場合や最良の場合の結果を特定することができます。また、平均や分散を計算することで、結果の中心やばらつきを把握することができます。
Excelモンテカルロシミュレーションの注意点
Excelモンテカルロシミュレーションを行う際には、以下の点に注意してください。 1. シミュレーションの試行回数が十分であることを確認してください。試行回数が少ないと、結果の信頼性が低くなります。 2. シミュレーションに使用する乱数が適切であることを確認してください。乱数の質が悪いと、結果に偏りが生じることがあります。 3. モデルの仮定や前提条件が現実に即していることを確認してください。仮定が間違っていると、シミュレーションの結果も誤ったものになります。
| 項目 | 説明 |
|---|---|
| モンテカルロシミュレーションの原理 | ランダムな試行を繰り返すことで確率分布に従った結果を得る |
| Excelでの実施方法 | 関数やマを利用してモデルを作成し、乱数を生成してシミュレーションを実行 |
| 活用事例 | プロジェクトリスク管理、ポートフォリオ分析、市場予測など |
| 結果の解釈方法 | 確率分布を解析し、平均や分散を計算する |
| 注意点 | 試行回数の十分さ、乱数の質、モデルの仮定や前提条件の妥当性 |
詳細情報
モンテカルロシミュレーションとは何ですか?
モンテカルロシミュレーションは、確率的シミュレーション手法の一つで、ランダムな事象を多数繰り返しシミュレーションすることで、未来の出来事を予測する方法です。この手法は、複数の不確実性要因が関与する問題に対して、数値的な予測を行うことができます。例えば、投資のリスク評価やプロジェクトのスケジュール管理など、さまざまな分野で利用されています。
Excelでモンテカルロシミュレーションを行う方法を教えてください。
Excelでモンテカルロシミュレーションを行うためには、まず、ランダムな数値を生成する関数を利用します。例えば、RAND関数を使用して、0から1までのランダムな数値を生成できます。このランダムな数値を、シミュレーション対象のパラメータに適用し、結果を計算します。この計算を何度も繰り返すことで、さまざまなシナリオをシミュレーションできます。最後に、シミュレーション結果を集計・分析し、未来予測を行います。
モンテカルロシミュレーションの実践例を一つ挙えてください。
実践例の一つとして、株式投資のリスク評価が挙げられます。株式の価格変動は、さまざまな要因によって影響を受けます。モンテカルロシミュレーションを用いることで、将来の株価の変動を予測することができます。例えば、過去の株価データをもとに、将来の株価の期待収益率やボラティリティを推定し、ランダムな数値を用いてシミュレーションを行います。シミュレーションを繰り返すことで、株価の変動の確率分布が得られ、リスク評価に役立てることができます。
モンテカルロシミュレーションの利点は何ですか?
モンテカルロシミュレーションの利点は、複数の不確実性要因が関与する問題に対して、数値的な予測を行うことができることです。また、シミュレーションを繰り返すことで、様々なシナリオを考慮することができるため、リスク評価や意思決定の質を向上させることができます。さらに、Excelのような一般的なソフトウェアを利用して、手軽にシミュレーションを行うことができることも、大きな利点です。

